Cum adantennaeQuaestio de qua homines maxime solliciti sunt est "Quomodo radiatio re vera efficitur?" Quomodo campus electromagneticus a fonte signi generatus per lineam transmissionis et intra antennam propagatur, et tandem ab antenna "separatur" ut undam in spatio libero formet.
1. Radiatio unius fili
Ponamus densitatem oneris, expressam ut qv (Coulomb/m³), uniformiter distributam esse in filo circulari cum area sectionis transversalis a et volumine V, ut in Figura 1 demonstratur.
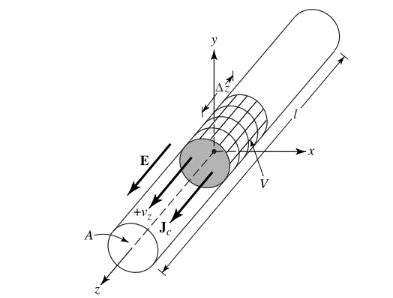
Figura 1
Summa electricitatis Q in volumine V in directione z celeritate uniformi Vz (m/s) movetur. Demonstrari potest densitatem currentis Jz in sectione transversali fili esse:
Jz = qv vz (1)
Si filum ex conductore ideali factum est, densitas currentiae Js in superficie fili est:
Js = qs vz (2)
Ubi *qs* est densitas oneris superficialis. Si filum tenuissimum est (idealiter, radius 0 est), fluxus electricus in filo exprimi potest ut:
Iz = ql vz (3)
Ubi ql (coulomb/metrum) est carica per unitatem longitudinis.
Filis tenuibus imprimis operam damus, et conclusiones ad tria exempla supradicta pertinent. Si fluxus electricus tempore variat, derivativum formulae (3) respectu temporis est ut sequitur:
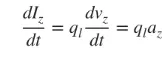
(IV)
az est acceleratio oneris. Si longitudo fili est l, (4) sic scribi potest:
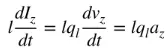
(V)
Aequatio (5) est relatio fundamentalis inter currentem et onus, et etiam relatio fundamentalis radiationis electromagneticae. Simpliciter dictum, ad radiationem producendam, necesse est currentem vel accelerationem (vel decelerationem) oneris tempore variantem adesse. Solemus currentem in applicationibus tempori harmonicis memorare, et onus saepissime in applicationibus transeuntibus memoratur. Ad accelerationem (vel decelerationem) oneris producendam, filum flecti, plicari, et discontinuum esse debet. Cum onus in motu tempori harmonico oscillat, etiam periodicam accelerationem (vel decelerationem) oneris vel currentem tempore variantem producet. Ergo:
1) Si sarcina non movetur, nulla erit electricitas neque radiatio.
2) Si sarcina celeritate constanti movetur:
a. Si filum rectum est et infinita longitudine, nulla radiatio est.
b. Si filum flectitur, complicatur, vel discontinuum est, ut in Figura 2 demonstratur, radiatio est.
3) Si onus per tempus oscillat, onus radiabit etiamsi filum rectum est.
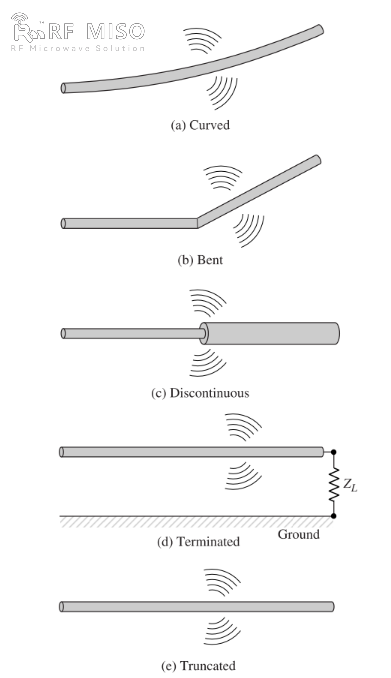
Figura II
Intellectus qualitativus mechanismi radiationis obtineri potest inspiciendo fontem pulsatum connexum filo aperto, quod per onus in extremo aperto suo connecti potest, ut in Figura 2(d) demonstratur. Cum filum initialiter excitatur, onera (electrones liberae) in filo in motum ponuntur a lineis campi electrici a fonte generatis. Cum onera accelerantur in extremo fontis fili et retardantur (acceleratione negativa relativa ad motum originalem) cum in extremo suo reflectuntur, campus radiationis in extremis eius et per reliquam partem fili generatur. Acceleratio onerarum per fontem vis externam perficitur, qui onera in motum ponit et campum radiationis associatum producit. Deceleratio onerarum in extremis fili perficitur viribus internis cum campo inducto associatis, quae causatur ab accumulatione onerarum concentratarum in extremis fili. Vires internae energiam acquirunt ex accumulatione onerarum cum velocitas eius ad nihilum decrescit in extremis fili. Ergo, acceleratio oneris propter excitationem campi electrici et retardatio oneris propter discontinuitatem vel curvam lenem impedantiae fili sunt mechanismi generationis radiationis electromagneticae. Quamquam et densitas currentis (Jc) et densitas oneris (qv) termini fontis in aequationibus Maxwellianis sunt, onus habetur quantitas fundamentalior, praesertim pro campis transeuntibus. Quamquam haec explicatio radiationis praecipue ad status transeuntes adhibetur, etiam ad radiationem status stabilis explicandam adhiberi potest.
Plura optima commendareproducta antennarumfabricatus abRFMISO:
2. Radiatio duorum filorum
Fontem tensionis electricae lineae transmissionis biconductorum, antennae coniunctae, ut in Figura 3(a) demonstratur, coniunge. Applicatio tensionis electricae lineae biconductorum campum electricum inter conductores generat. Lineae campi electrici in electrones liberos (facile ab atomis separatos) singulis conductoribus coniunctos agunt et eos moveri cogunt. Motus electricorum currentem generat, qui vicissim campum magneticum generat.
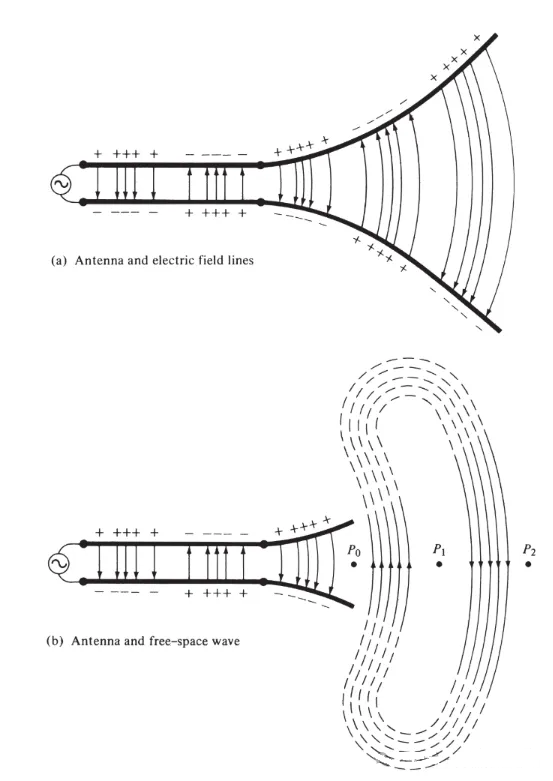
Figura III
Accepimus lineas campi electrici oneribus positivis incipere et oneribus negativis terminari. Scilicet, etiam oneribus positivis incipere et ad infinitum terminari possunt; vel ab infinito incipere et oneribus negativis terminari; vel circulos clausos formare qui neque ullis oneribus incipiunt neque terminantur. Lineae campi magnetici semper circulos clausos circa conductores currentem portantes formant, quia nullae oneres magneticae in physica exstant. In quibusdam formulis mathematicis, oneres magnetici aequivalentes et currentes magnetici introducuntur ad dualitatem inter solutiones fontes potentiae et magneticos implicantes demonstrandam.
Lineae campi electrici inter duos conductores ductae distributionem oneris demonstrare adiuvant. Si fontem tensionis sinusoidalem esse supponimus, campum electricum inter conductores etiam sinusoidalem esse exspectamus, cum periodo aequali periodi fontis. Magnitudo relativa roboris campi electrici densitate linearum campi electrici repraesentatur, et sagittae directionem relativam (positivam vel negativam) indicant. Generatio camporum electricorum et magneticorum tempore variantium inter conductores undam electromagneticam format quae per lineam transmissionis propagatur, ut in Figura 3(a) demonstratur. Unda electromagnetica antennam cum onere et currente correspondente intrat. Si partem structurae antennae removemus, ut in Figura 3(b) demonstratur, unda spatii liberi formari potest "connectendo" fines apertos linearum campi electrici (lineis punctatis monstratis). Unda spatii liberi etiam periodica est, sed punctum phasis constantis P0 celeritate lucis extrorsum movetur et distantiam λ/2 (ad P1) in dimidio tempore percurrit. Prope antennam, punctum phasis constantis P0 celerius quam celeritas lucis movetur et celeritatem lucis accedit in punctis ab antenna remotis. Figura 4 distributionem campi electrici in spatio libero antennae λ/2 apud t = 0, t/8, t/4, et 3T/8 ostendit.
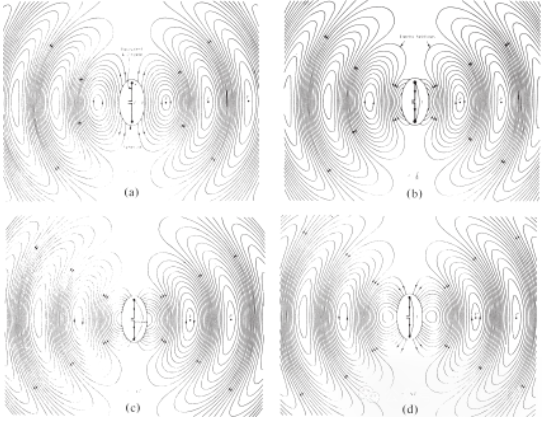
Figura 4 Distributio campi electrici in spatio libero antennae λ∕² apud t = 0, t/8, t/4 et 3T/8.
Nescitur quomodo undae directae ab antenna separentur et tandem formentur ut in spatio libero propagentur. Undas directas et in spatio libero cum undis aquae comparare possumus, quae a lapide in aquam tranquillam demisso vel aliis modis causari possunt. Postquam perturbatio in aqua incipit, undae aquae generantur et extrorsum propagari incipiunt. Etiam si perturbatio cessat, undae non cessant sed porro propagari pergunt. Si perturbatio perseverat, novae undae perpetuo generantur, et propagatio harum undarum post alias undas segniter procedit.
Idem valet de undis electromagneticis a perturbationibus electricis generatis. Si perturbatio electrica initialis a fonte brevis durationis est, undae electromagneticae generatae intra lineam transmissionis propagantur, deinde antennam ingrediuntur, et tandem ut undae spatii liberi radiant, etiamsi excitatio iam non adest (sicut undae aquae et perturbatio quam creaverunt). Si perturbatio electrica continua est, undae electromagneticae continue existunt et eas prope sequuntur durante propagatione, ut in antenna biconica in Figura 5 ostensa demonstratur. Cum undae electromagneticae intra lineas transmissionis et antennas sunt, earum existentia cum existentia oneris electrici intra conductorem coniungitur. Attamen, cum undae radiantur, circulum clausum formant et nulla onus est ad earum existentiam conservandam. Hoc nos ad conclusionem ducit:
Excitatio campi accelerationem et retardationem oneris requirit, sed conservatio campi accelerationem et retardationem oneris non requirit.
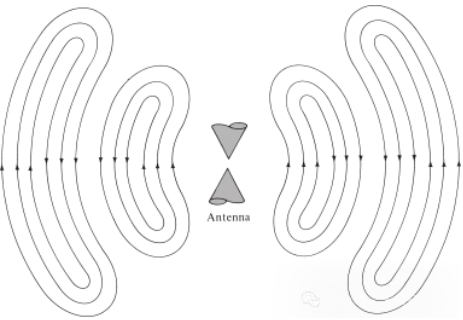
Figura V
3. Radiatio Dipolaris
Conamur explicare mechanismum quo lineae campi electrici ab antenna separantur et undas in spatio libero formant, antennam dipolarem ut exemplum sumimus. Quamquam explicatio simplicior est, etiam hominibus permittit intuitive videre generationem undarum in spatio libero. Figura 6(a) ostendit lineas campi electrici generatas inter duo brachia dipoli cum lineae campi electrici extrorsum moventur λ∕4 in prima parte cycli. In hoc exemplo, ponamus numerum linearum campi electrici formatarum esse 3. In sequenti parte cycli, tres lineae campi electrici originales moventur aliud λ∕4 (in summa λ∕2 a puncto initiali), et densitas oneris in conductore incipit decrescere. Consideri potest formata esse introductione oneris oppositorum, quae onus in conductore tollent in fine primae partis cycli. Lineae campi electrici generatae a oneribus oppositis sunt 3 et moventur distantiam λ∕4, quod lineis punctatis in Figura 6(b) repraesentatur.
Resultatum ultimum est tres lineas campi electrici deorsum spectantes in prima distantia λ∕⁴ et totidem lineas campi electrici sursum spectantes in secunda distantia λ∕⁴. Cum nulla sit carica netta in antenna, lineae campi electrici cogendae sunt ut a conductore separantur et inter se coniungantur ut circulum clausum forment. Hoc in Figura 6(c) demonstratur. In secunda parte, idem processus physicus sequitur, sed nota directionem esse oppositam. Post hoc, processus repetitur et in infinitum pergit, distributionem campi electrici similem Figurae 4 formans.
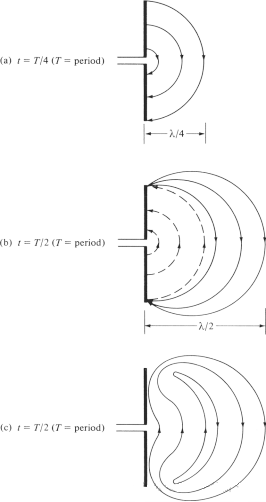
Figura VI
Ut plura de antennis discas, quaeso visita:
Tempus publicationis: Iun-XX-MMXXIV










