Polarizatio una ex proprietatibus fundamentalibus antennarum est. Primum polarizationem undarum planarum intellegere debemus. Deinde de generibus principalibus polarizationis antennarum disserere possumus.
polarizatio linearis
Incipiemus intellegere polarizationem undae electromagneticae planae.
Unda electromagnetica plana (EM) plures proprietates habet. Prima est quod vis in unam directionem progreditur (nullum campum in duabus directionibus orthogonalibus mutatur). Secunda, campus electricus et campus magneticus inter se perpendiculares et orthogonales sunt. Campi electrici et magnetici perpendiculares sunt directioni propagationis undae planae. Exempli gratia, considera campum electricum unius frequentiae (campum E) datum ab aequatione (1). Campus electromagneticus in directione +z progreditur. Campus electricus in directione +x dirigitur. Campus magneticus est in directione +y.
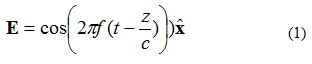
In aequatione (1), notationem observa: . Hic est vector unitatis (vector longitudinis), qui dicit punctum campi electrici esse in directione x. Unda plana illustratur in Figura 1.
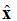
figura 1. Repraesentatio graphica campi electrici in directionem +z percurrentis.
Polarisatio est vestigium et forma propagationis (cimae lineae) campi electrici. Exempli gratia, considera aequationem campi electrici undae planae (1). Observabimus positionem ubi campus electricus est (X,Y,Z) = (0,0,0) pro functione temporis. Amplitudo huius campi in Figura 2 depingitur, pluribus temporibus. Campus oscillat ad frequentiam "F".
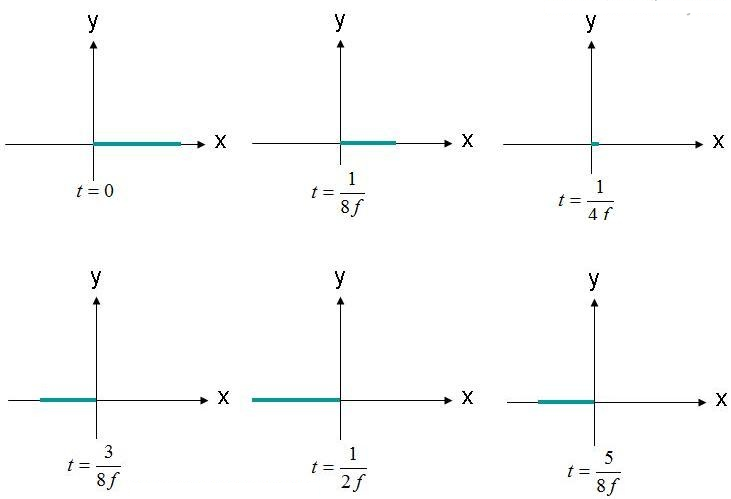
figura 2. Campum electricum (X, Y, Z) = (0,0,0) temporibus diversis observa.
Campus electricus in origine observatur, amplitudine huc illuc oscillans. Campus electricus semper secundum axem x indicatum est. Cum campus electricus secundum lineam unicam servetur, hic campus polarizatio lineari dici potest. Praeterea, si axis X solo parallelus est, hic campus etiam polarizatio horizontalis describitur. Si campus secundum axem Y orientatur, unda polarizatio verticalis dici potest.
Undae polarizatae lineariter non necesse est ut secundum axem horizontalem vel verticalem dirigantur. Exempli gratia, unda campi electrici cum vinculo secundum lineam iacente, ut in Figura 3 monstratur, etiam lineariter polarizata esset.
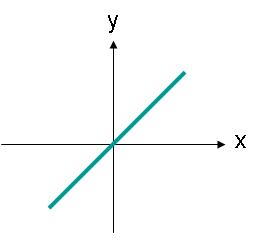
imago 3. Amplitudo campi electrici undae polarizatae lineariter cuius trajectoria est angulus.
Campus electricus in Figura 3 aequatione (2) describi potest. Nunc campi electrici et pars x et y adsunt. Ambae partes magnitudine aequales sunt.
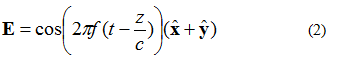
Una res notanda de aequatione (2) est pars xy et campi electronici in secundo gradu. Hoc significat ambas partes eandem amplitudinem omni tempore habere.
polarizatio circularis
Nunc ponamus campum electricum undae planae dari per aequationem (3):
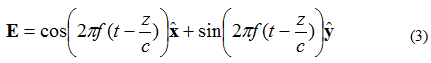
Hoc in casu, elementa X et Y 90 gradibus a phase discrepant. Si campus iterum ut antea ut (X, Y, Z) = (0,0,0) observetur, curva campi electrici contra tempus apparebit ut infra in Figura 4 monstratur.
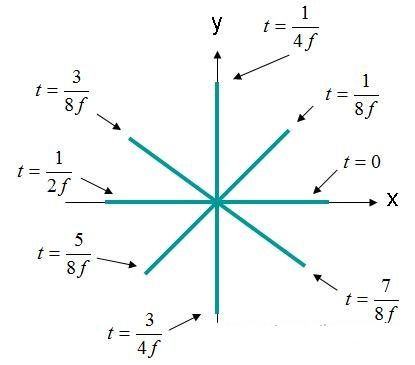
Figura 4. Robur campi electrici (X, Y, Z) = (0,0,0) dominium EQ. (3).
Campus electricus in Figura 4 circulo rotatur. Hoc genus campi unda circulariter polarizata describitur. Ad polarizationem circularem, haec criteria implenda sunt:
- Norma pro polarizatione circulari
- Campus electricus duas componentes orthogonales (perpendiculares) habere debet.
- Partes orthogonales campi electrici amplitudines aequales habere debent.
- Partes quadraturae nonaginta gradibus a phase discrepantiae esse debent.
Si per imaginem Undae Figurae 4 progredimur, rotatio campi dicitur esse contrahorologica et dextra circulariter polarizata (RHCP). Si campus dextra rotatur, campus erit polarizatio circularis sinistra (LHCP).
Polarizatio elliptica
Si campus electricus duas partes perpendiculares, 90 gradibus a phase discrepantes sed magnitudinis aequalis, habet, campus elliptice polarizabitur. Considerando campum electricum undae planae in directione +z progredientis, aequatione (4) descriptum:
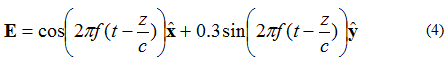
Locus puncti ubi apex vectoris campi electrici se collocabit in Figura 5 datur.
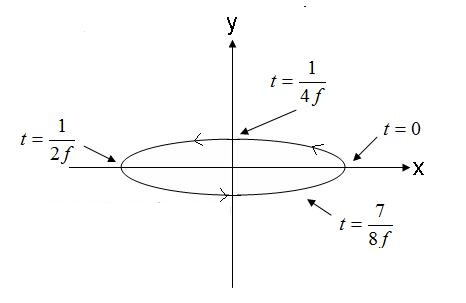
Figura 5. Campus electricus undae polarizationis ellipticae promptae. (4).
Campus in Figura 5, contra horologii directionem progrediens, ellipticus dextrorsum esset si extra velo progrederetur. Si vector campi electrici in directionem oppositam rotatur, campus elliptice laevorsum polarizabitur.
Praeterea, polarizatio elliptica ad eccentricitatem suam refertur. Ratio eccentricitatis ad amplitudinem axium maioris et minoris. Exempli gratia, eccentricitas undae ex aequatione (4) est 1/0.3 = 3.33. Undae elliptice polarizatae ulterius describuntur directione axis maioris. Aequatio undae (4) axem habet praecipue ex axe x constantem. Nota axem maiorem posse esse ad quemvis angulum planum. Angulus non requiritur ut axi X, Y vel Z conveniat. Denique, interest notare polarizationem circularem et linearem casus speciales polarizationis ellipticae esse. Unda elliptice polarizata eccentrica 1.0 est unda circulariter polarizata. Undae elliptice polarizatae cum eccentricitate infinita. Undae lineariter polarizatae.
Polarizatio antennae
Nunc cum campos electromagneticos undarum planarum polarizatarum novimus, polarizatio antennae simpliciter definitur.
Polarisatio Antennae Aestimatio campi longinqui antennae, polarizatio campi radiati resultantis. Quapropter antennae saepe ut "lineariter polarizatae" vel "antennae dextrorsae circulariter polarizatae" enumerantur.
Haec simplex notio magni momenti est ad communicationes antennarum. Primo, antenna polarizata horizontaliter cum antenna polarizata verticaliter non communicabit. Propter theorema reciprocitatis, antenna transmittit et recipit eodem modo. Ergo, antennae polarizatae campos polarizatos verticaliter transmittunt et recipiunt. Ergo, si antennam polarizatam verticaliter et horizontaliter transmittere conaris, nulla receptio erit.
In casu generali, pro duabus antennis lineariter polarizatis quae inter se angulo ( ) rotantur, iactura potentiae ob hanc discrepantiam polarizationis factore iacturae polarizationis (PLF) describetur:
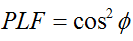
Ergo, si duae antennae eandem polarizationem habent, angulus inter campos electronicos radiantes nullus est, et nulla potentiae iactura propter discrepantiam polarizationis est. Si una antenna verticaliter polarizatur et altera horizontaliter, angulus 90 graduum est, et nulla potentia transferetur.
NOTA: Movendo telephonum supra caput ad angulos diversos, explicatur cur receptio interdum augeri possit. Antennae telephonorum cellularium plerumque polarizantur lineariter, ergo rotatio telephoni saepe polarizationem telephoni congruere potest, ita receptionem emendans.
Polarisatio circularis est proprietas desiderabilis multarum antennarum. Ambae antennae sunt circulariter polarizatae nec amissionem signalis propter discrepantiam polarizationis patiuntur. Antennae in systematibus GPS adhibitae sunt polarizatio circularis dextra.
Nunc ponamus antennam polarizatam lineariter undas polarizatas circulariter accipere. Aequivalens, ponamus antennam polarizatam circulariter undas polarizatas lineariter accipere conari. Quid est factor damni polarizationis resultans?
Memento polarizationem circularem re vera esse duas undas orthogonales lineariter polarizatas, 90 gradibus a phase discrepantes. Ergo, antenna lineariter polarizata (LP) tantum componentem phasis undae circulariter polarizatae (CP) recipiet. Ergo, antenna LP iacturam propter discrepantiam polarizationis 0.5 (-3dB) habebit. Hoc verum est quocumque angulo antenna LP rotetur. Ergo:
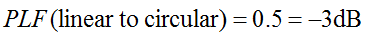
Factor amissionis polarizationis interdum efficacia polarizationis, factor discrepantiae antennae, vel factor receptionis antennae appellatur. Haec omnia nomina ad eandem notionem referuntur.
Tempus publicationis: XXII Decembris MMXXIII







